New 2 Hour Format

Starting October 4th, Metroplex Math Circle lectures will take place from 2:00 to 4:00. We are hoping that the new 2 hour time will produce fewer conflicts with the busy weekend activities of our many students. Because the length of the lectures has been reduced we urge everyone to arrive for a prompt start at 2:00.

After 4:00, students may want to spend some time talking with one another or asking questions of our speakers. Parents might also use this informal time for discussion of the Math Circle or other relevant topics.

Read Full Post »

Alicia Prieto Langarica – “Cryptography”

October 4th, we will review the history of cryptography starting with the classic methods, medieval techniques, cryptographic mechanical machines and finishing with contemporary cryptographic methods. We will discuss the advantages and disadvantages of each method and we will try to come up with different cryptographic methods of our own.

Ms. Langarica is a mathematics Phd student at The University of Texas at Arlington. She has a BS in Applied Mathematics from the Univestity of Texas at Dallas and was a contestant in the Mexican Mathematics Olympiads for 5 years where she received one national silver medal and two gold medals. Since then, she has been involved continuously in mathematics Olympiads as a trainer and problem writer.

Read Full Post »

Dr. Bennette Harris Today!

Please join us today for a lecture by Dr. Bennette Harris on “Computer Data Encryption – Decrypted.” We will meet at 2:00 in our usual location: room 2.410 of the Engineering and Computer Sciences South (ECSS) building on the UT Dallas campus. The building is at the corner of Drive A and Rutford.

As we learned from Richard Rusczyk last week, computer science relies far more on the discreet math taught at Math Circles and used in contests rather than the standard curriculum. If a student wants the option of pursuing a career in technology, learning the topics introduced by Dr. Harris can be a great head start.

Read Full Post »

September 20th Photos

Following are some pictures of the first MMC meeting of the 2008-2009 season.

As you can see we have an excellent facility thanks to the generosity of UT Dallas. What is harder to see is that we filled every seat in a room with capacity >100.

Read Full Post »

Dr. Bennette Harris – Problem Set 2

Here is the continuation of Dr. Bennett Harris’ problems to warm us up before his lecture on September 27th. Congratulations to Dominic for being the first to answer the previous set of problems in the comments. Another happy discovery is the fact that WordPress, which hosts this site, supports the use of code!

Problems

A solution for each of the following should either give the correct answer, or a technique for determining the answer in reasonable time with the assistance of a calculator.

6. Crack this secret message: “uifsfaxjmmacfabmnptuaopaqsppgtaupebz”

7. Code the alphabet a=0, b=1, …, z=25, space=26. We will encrypt each letter of the alphabet by mapping it to the letter 3 farther along in the alphabet. Thus, a maps to d, b maps to e, and so forth. The message “a bat is fat” would be encrypted as “dcedwclvciodw” in this scheme. Find a mathematical function f(x) such that y=f(x) gives the correct encryption for every value x = 0,1,2,…,26. Test your function by encrypting “the toy boat floats”.

8. The purpose of these two questions is to provide points of comparison for the questions that follow:
How many particles are there in the known universe?
How many microseconds have elapsed since the beginning of the universe?

9. How long (approximately will do) would it take to calculate at 1,000,000 calculations per second? How many digits does the answer have? If p is 200 digits long, and if q is 200 digits long, about how many digits are there in pq?

10. The number 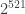– 1 is known to be prime. Estimate how long it would take a computer to demonstrate this by repeated division, at 1,000,000 divisions per second.

Read Full Post »

Dr. Bennette Harris – Problem Set 1

This Saturday’s (9/27) Math Circle lecture by Dr. Bennett Harris on “Computer Data Encryption – Decrypted” promises to be a great combination of number theory and applied math. To warm up the students, Dr. Harris forwarded some problems that I will post in two parts. Feel free to offer solutions in the comments or to just work them on your own. Full solutions will be made available at the next Math Circle.

Problems

A solution for each of the following should either give the correct answer, or a technique for determining the answer in reasonable time with the assistance of a calculator.

1. How many prime numbers are there? Prove your answer.

2. What is the largest number you must test to demonstrate that 83 is prime?

3. What is the smallest 5-digit prime? How could you find this number?

4. Is 1234567890 prime? What about 123456789?

5. Assume an alphabet with 26 letters (plus a blank space). A substitution cipher is a one-to-one mapping of this alphabet onto itself. How many such substitution ciphers are there?

Read Full Post »

Richard Rusczyk Recap

The first Math Circle of the 2008-2009 season succeeded on multiple levels. In its third year, Metroplex Math Circle finally exceeded the capacity of its current (large) lecture hall with over 100 students, teachers and parents in attendance. We were pleased to see many friends return, but even more new faces who were discovering Math Circles for the first time.

Comparative Advantage

Richard Rusczyk’s talks also exceeded all expectations. His first lecture was on the concept of comparative advantage and the benefits of free trade which many adults fail to grasp. Like many lessons in Math Circle, Mr. Rusczyk allowed the students to discover the meaning of the concept by playing out a game between two imagined countries. “Games” and the importance of “play” would be stressed throughout the day.

Option Pricing

The second segment introduced the audience to the principles of market prices and call options. With the current turmoil on Wall Street, parents were just as interested in this topic as the students. Mr. Rusczyk presented the students with a problem that he would use when he was recruiting for D.E. Shaw. Only the best students from elite schools ever made it to this stage in the interview process and apparently all but a handful (accomplished problem solvers) ever answered the problem correctly.

Life After MATHCOUNTS

In his final lecture, Richard Rusczyk sent students, parents and teachers home with a great deal to consider. He spoke very frankly and persuasively about the short comings of the standard school curriculum. But rather than just criticize, he also laid out concrete ways that students, parents and teachers can all improve the situation.

We won’t attempt to summarize this excellent talk particularly since an early version of the slides can be accessed below. However, a couple of themes should be highlight. First was his emphasis on play and the importance of giving students the time and freedom to work on challenging problems. A second theme was the importance of building a math community for young problem solvers, and the central role that a Math Circle can play. Finally, Mr. Rusczyk endorsed what many of us have already discovered, that Dr. Titu Andreescu’s books and leadership have been critical to the Renaissance in global problem solving.

Richard Rusczyk has committed himself to fulfilling the principles in his presentation by founding the Art of Problem Solving. Please take the time to see his presentation and the other excellent resources he has collected and developed.

Read Full Post »

Richard Rusczyk Today!

The day has finally arrived, the first lecture of the MMC 2008-2009 season!  We are very pleased to have Richard Rusczyk join us from San Diego.  Richard is the author of many books used by accomplished problem solvers for individual study or as the backbone of a classroom course.  One example is his new book Introduction to Algebra.

Introduction to Algebra

Learn the basics of algebra from former USA Mathematical Olympiad winner and Art of Problem Solving founder Richard Rusczyk. Topics covered in the book include linear equations, ratios, quadratic equations, special factorizations, complex numbers, graphing linear and quadratic equations, linear and quadratic inequalities, functions, polynomials, exponents and logarithms, absolute value, sequences and series, and much more!

Read Full Post »

Coming Prepared to Math Circle

Math Circle is a very inexpensive activity since all of the costs are generously underwritten by UT Dallas.  The only materials needed are pencil and paper.  Calculators are not necessary and not encouraged.

Some students find it useful to have a math notebook or a binder to collect notes and handouts from various sessions.  At the end of a semester these notes can be very useful for contest preparation or further study.

Read Full Post »

Who are the Olympians?

Our friends at SDMC provide a link to a fascinating study at the Center for Mathematics Education. The PowerPoint presentation linked below provides some interesting demographic research on accomplished problem solvers.

“Mathematical Olympians: Who are they, where are they from, and how did they get where they are?”,

The research sets out to answer the following question:

What aspects of the in-school and out of school experiences of IMO caliber students can be identified as promising for the encouragement of a broader population of students into sustained and advanced study of mathematics in secondary school and beyond?

Of particular interest is the strong role played by the family, the school, the challenge of contests and mentors (slide 15). Metroplex Math Circle attempts to bring all 4 factors together to help our students to achieve their full potential.

Read Full Post »